MAYO

MARTES 3 DE MAYO DEL 2016 

Recta determinada por dos planos 

Para encontrar la recta que se genera en la intersección de los dos planos se debe realizar el producto cruz de dos vectores de cada plano y el resultado sera la nueva ecuación de la recta que queremos encontrar.

Ecuación del haz de planos.

El haz de puntos es el conjunto de planos que pasan por la misma recta

Para encontrar esta ecuación es necesario conocer las n ecuaciones de planos y multiplicarlos por valores conocidos que sean diferentes de cero. 

Después se procede a sumar todas las ecuaciones y el resultado obtenido es nuestra nueva ecuación del haz de planos. 

Ecuación Vectorial de la superficie esférica.

Para encontrar la ecuacion vectorial vamos a partir de que se conocen las coordenadas del centro, las coordenadas de cualquier punto de la superficie de la esfere y conocemos la distancia del radio

Hipotesis:                                                      Tesis:

C (x,y,z)                                                          Ecuación Vectorial de la esfera

M (a,b,c)

Radio= R

1.-CM=R

2.-(CM)^2=R^2

3.- (CM)^2= (r-ro) ^2         =====> Vectores posicion

2=3

(r-ro) ^2  = R^2       =====> Ecuación Vectorial de la esfera

En el siguiente vídeo esta la demostración de como obtener la ecuación general de la esfera

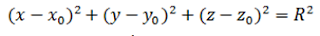
JUEVES 5 DE MAYO DEL 2016

Cilindros y Superficies Cuadráticas.

En el siguiente video hay ejemplos delas gráficas de las superficies cuadráticas.

Analisis Grafico de las Superficies Cuadraticas

Para encontrar un bosquejo de nuestra superficie debemos realizar 4 pasos.

1. Intersección de la superficie con los ejes coordenados.  Es decir los puntos de corte de los ejes 
2. Intersección de la superficie con los planos coordenados. Aquí vamos a encontrar las superficies que se dibujan dentro de cada plano (XOY, XOZ, YOZ)
3. Intersección de la superficie con los planos paralelos a los planos coordenados. Al igual que el punto anterior debemos ver cuantos planos paralelos se generan. Esto los vamos a lograr igualando a un valor k a la variable que le corresponda en el plano.
4. Bosquejo de la gráfica de la superficie.

En este vídeo hay una breve explicación de como se logra el punto 2.

JUEVES 12 DE MAYO DEL 2016

Funciones Vectoriales de variable real

Llamamos función vectorial de la variable real "t" a toda correspondencia  F de I subconjunto de los Reales en R^n.

               F: I==>R^n

                   t ==>F(t)=(f1(t);f2(t);.......;fn(t))

                   Donde fk(t) son funciones reales

• El dominio de la función es la Intersección de todos los dominios de los componentes del vector.
• El rango de la función es la Unión de todos los rangos de los componentes del vector.

MARTES 17 DE MAYO DEL 2016

Operaciones con funciones vectoriales 

Las operaciones principales son:

• (F+G)(t)=F(t)+G(t); ∀ t ∈ Dom F ∩ Dom G
• (αF)(t)=αF(t); α ∈ R; ∀ t ∈ Dom F
• <F\G>(t)=<F(t)\G(t)>= ∑ fi(t)gi(t); ∀ t ∈ Dom F ∩ Dom G
• ││F(t)││= √(<F(t)\F(t)>)=√ ∑ fi(t)^2; ∀ t ∈ Dom F
• Si n=3; ∀ t ∈ Dom F ∩ Dom G                                                                                                           (F×G)(t)=(F(t)×G(t))
• (F o h(t))=F(h(t)); ∀ t ∈ Dom F ∩ Dom h

Limites y continuidad 

• Existirá el límite de una función vectorial siempre y cuando existan los límites de cada una de sus funciones componentes.
• Los límites de funciones vectoriales siguen las reglas y cumplen las mismas propiedades de los límites de las funciones reales escalares.
• Una función r(t) será continua en un punto a, solo si el límite de r(t) cuando t tiende a "a" es igual a r(a).
• r(t) es continua en "a", si y solo si f(t), g(t), h(t) son continuas cuando t tiende a "a".

JUEVES 19 DE MAYO DEL 2016

Derivación de funciones vectoriales

• Para calcular la derivada de una función vectorial se debe derivar cada una de sus componentes.
• Se aplican las propiedades y las reglas de derivación de las funciones reales escalares.

Interpretacion geometrica

          Se considera a F'(t) como el vector tangente a la curva en el punto t

Interpretacion Fisica

        

1. F'(t) corresponde al vector velocidad y su modulo como la velocidad escalar
2. F''(t) corresponde al vector aceleración y su modulo como la aceleracion escalar

Integración de funciones vectoriales

Cumple las mismas propiedades de las Integrales Reales.

Longitud de arco y curva

MARTES 24 DE MAYO DEL 2016

Reparametrizacion

Toda curva alabeada C se representa por mas de una función vectorial 

por ejemplo 

                  r1(t)=(t,t^2,t^3); 1≤t≤2

                  se puede representar por 

                  r2(t)=(e^u,e^2u,e^3u); 0≤u≤ln2

                  si t= e^u

La longitud de arco es independiente de la reparametrizacion que se utilize.

Suponga que es una curva suave por partes dada por F(t) = f(t)î + g(t)j+ h(t); a ≤ t ≤ b donde r'(t) es continua y c es recorrido una vez cuando t se incrementa desde "a" hasta "b" se define: s(t) = a la integral del módulo de r'(u) desde 0 a t, siendo s(t) la longitud de arco de c entre r(a) y r(b).

Curvatura

• Una parametrización se dice suave en un intervalo I, si r(t) es continua y r'(t) es diferente de 0 en I.
• Una curva suave no tiene puntos agudos o cúspides, cuando gira el vector tangente, lo hace en forma continua.
• El vector tangente unitario indica la dirección de la curva c.
• La curva c se define como                                                                                                    k = |dT^/ds|                                                                                                                 donde dT^representa el vector tangente unitario.

JUEVES 26 DE MAYO DEL 2016

Vectores normales y binormales

• El principal vector normal se define como:                                                                                                                                                                                                                                                   N(t)= T'(t)                                                                                                                                                  |T'(t)| 
• El vector binormal se define

             B(t) = T(t)×N(t)

Asi se formaria un tiedro movil compuesto por 

1. Plano Osculador: T  ∧ N
2. Plano Normal Principal: N  ∧ B
3. Plano Rectificante: T ∧ B

Aqui les dejo un video de la aplicacion de los vectores Tangenciales, Normales y Binormales

Plano Osculador

Vector Normal: B=(Bx,By,Bz)

Po(Xo,Yo,Zo)

(X-Xo,Y-Yo,Z-Zo) · (Bx,By,Bz)=0

Bx(X-Xo)+By(Y-Yo)+Bz(Z-Zo)=0  ===> Ec. Plano Osculador

Plano Normal Principal 

Vector Normal: T=(Tx,Ty,Tz)

Po(Xo,Yo,Zo)

(X-Xo,Y-Yo,Z-Zo) · (Tx,Ty,Tz)=0

Tx(X-Xo)+Ty(Y-Yo)+Tz(Z-Zo)=0  ===> Ec. Plano Normal Principal

Plano Rectificante

Vector Normal: N=(Nx,Ny,Nz)

Po(Xo,Yo,Zo)

(X-Xo,Y-Yo,Z-Zo) · (Nx,Ny,Nz)=0

Nx(X-Xo)+Ny(Y-Yo)+Nz(Z-Zo)=0  ===> Ec. Plano Rectificante 

Funciones de varias variables

f:R^n⇒R

si n=2

f:R^2⇒R

(x,y)⇒z=f(x,y)

Donde x, y son las variables independientes 

           z es la variable dependiente 

El dominio de la función se encuentra en todo el plano o en una parte del plano 

El rango de la función se encuentra en todos los reales o en una parte de los reales

MARTES 31 DE MAYO DEL 2016

Analisis del dominio de definicion o dominio de existencia 

Para el analisis de los dominios vamos a trabajar con 3 puntos que son:

• Demostrarlo analiticamente
• Demostrarlo graficamente
• Representarlo descriptivamente 

E aqui un ejemplo de como obtener el dominio de nuestra funcion.

Y Aqui otro ejemplo

Graficas y Curvas de Nivel 

Para representar la grafica de una funcion f(x,y) se requiere de un sistema coordenado (x,y,z) en R^3

Definicion

• Si f es una funcion de dos variables con dominio D entoncs la grafica de f es el conjunto de todos los puntos (x,y,z) en R^3 tal que z=f(x,y) y (x,y) esta en D.
• La grafica de f(x,y) es una superficie en R^3

Si tenemos una función de tres variables f(x,y,z), su Dominio nos representa una region de R^3 o todo R^3.

Ademas no es posible representar gráficamente las funciones de 3 o mas variables independientes.

Curvas de Nivel 

Las curvas de nivel de una funcion f de dos variables son las curvas cuyas ecuacione son f(x,y)=k, donde k es una constante(en el rango de f)

Ejm:

La interseccion del plano z=k con la superficie z=f(x,y) se denomina CURVA  DE CONTORNO

La proyeccion de estas curvas de controno en el plano XOY son las CURVAS DE NIVEL f(x,y)=k de la funcion f.

Si w=f(x,y,z) entoncs si w=k(constante)

f(x,y,z)=k representa una superficie de nivel.

Si w=f(x,y,z, k) donde w es una constante

representa una hipersuperficie de nivel.